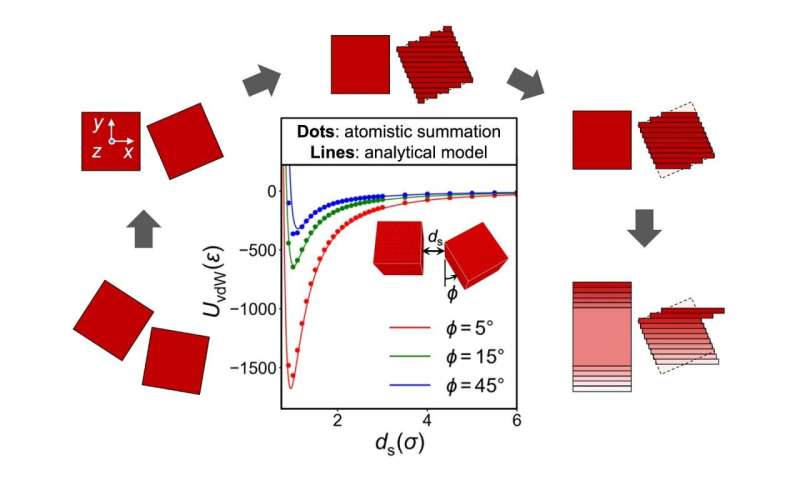
Overzicht van de aanpak die wordt gebruikt voor het afleiden van analytische uitdrukkingen voor het interparticle van der Waals-interactiepotentieel voor gefacetteerde nanodeeltjes. Het model doorloopt een reeks vereenvoudigingen. Een blok wordt genormaliseerd in een standaardpositie. Het andere blok wordt dan verondersteld een groep staven te zijn. Alle staven buiten de grenzen van het eerste blok worden als verwaarloosbaar beschouwd. Het eerste blok wordt verschoven om gecentreerd te zijn op elke staaf van het tweede blok terwijl de krachten worden berekend en opgeteld. Krediet: Gaurav Arya, Duke University
Materiaalwetenschappers van Duke University hebben een vereenvoudigde methode bedacht om de aantrekkingskracht te berekenen die ervoor zorgen dat nanodeeltjes zichzelf assembleren tot grotere structuren.
Met dit nieuwe model, vergezeld van een grafische gebruikersinterface die zijn kracht laat zien, kunnen onderzoekers voorheen onmogelijke voorspellingen doen over hoe nanodeeltjes met een grote verscheidenheid aan vormen met elkaar zullen interageren. De nieuwe methode biedt mogelijkheden om dergelijke deeltjes rationeel te ontwerpen voor een breed scala aan toepassingen, van het benutten van zonne-energie tot het aansturen van katalytische reacties.
De resultaten verschijnen op 12 november online in het tijdschrift Nanoschaal Horizons.
“Gefacetteerde nanodeeltjes kunnen leiden tot nieuw assemblagegedrag, dat in het verleden niet is onderzocht”, zegt Brian Hyun-jong Lee, een afgestudeerde student werktuigbouwkunde en materiaalkunde aan Duke en eerste auteur van het artikel. “Kubussen, prisma’s, staven enzovoort vertonen allemaal verschillende afstands- en oriëntatieafhankelijke interacties tussen de deeltjes die kunnen worden gebruikt om unieke deeltjesassemblages te creëren die men niet kan verkrijgen door zelfassemblage van bolvormige deeltjes.”
“Elke keer dat ik de laatste reeks gepubliceerde artikelen over nanotechnologie doorneem, zie ik een nieuwe toepassing van dit soort nanodeeltjes”, voegt Gaurav Arya, universitair hoofddocent werktuigbouwkunde en materiaalkunde bij Duke toe. “Maar het nauwkeurig berekenen van de krachten die deze deeltjes van zeer dichtbij samenbrengen, is uiterst rekenkundig duur. We hebben nu een aanpak gedemonstreerd die die berekeningen miljoenen keren versnelt, terwijl er slechts een kleine hoeveelheid nauwkeurigheid verloren gaat.”
De krachten die tussen nanodeeltjes werken, worden van der Waals-krachten genoemd. Deze krachten ontstaan door kleine, tijdelijke verschuivingen in de dichtheid van elektronen die in een baan om atomen draaien volgens de complexe wetten van de kwantumfysica. Hoewel deze krachten zwakker zijn dan andere intermoleculaire interacties zoals coulombische krachten en waterstofbruggen, zijn ze alomtegenwoordig en werken ze tussen elk atoom, waarbij ze vaak de netto interactie tussen deeltjes domineren.
Om dergelijke krachten tussen deeltjes goed te kunnen verklaren, moet men de Van der Waalskracht berekenen die elk atoom in het deeltje uitoefent op elk atoom in een nabijgelegen deeltje. Zelfs als beide deeltjes in kwestie minuscule blokjes waren met een grootte kleiner dan 10 nanometer, zou het aantal berekeningen dat al dergelijke interatomaire interacties optelt in de tientallen miljoenen liggen.
Het is gemakkelijk in te zien waarom dit keer op keer proberen te doen voor duizenden deeltjes die zich op verschillende posities en in verschillende oriëntaties bevinden in een simulatie van meerdere deeltjes snel onmogelijk wordt.
“Er is veel werk verzet om een sommatie te formuleren die dicht bij een analytische oplossing komt”, zei Arya. “Sommige benaderingen behandelen deeltjes als bestaande uit oneindig kleine blokjes die aan elkaar zijn geplakt. Andere proberen de ruimte te vullen met oneindig dunne cirkelvormige ringen. Hoewel deze volumediscretisatiestrategieën onderzoekers in staat hebben gesteld om analytische oplossingen te vinden voor interacties tussen eenvoudige deeltjesgeometrieën zoals parallelle platte oppervlakken of bolvormige deeltjes, dergelijke strategieën kunnen niet worden gebruikt om de interacties tussen gefacetteerde deeltjes te vereenvoudigen vanwege hun complexere geometrieën. “
Om dit probleem te omzeilen, kozen Lee en Arya een andere benadering door verschillende vereenvoudigingen aan te brengen. De eerste stap houdt in dat het deeltje wordt voorgesteld als zijnde niet samengesteld uit kubusvormige elementen, maar uit staafvormige elementen van verschillende lengtes die op elkaar zijn gestapeld. Het model gaat er vervolgens van uit dat staafjes waarvan de uitsteeksels buiten de geprojecteerde grens van het andere deeltje vallen, een verwaarloosbare bijdrage leveren aan de totale interactie-energie.
De energieën die door de resterende staven worden bijgedragen, worden verder verondersteld gelijk te zijn aan de energieën van staven van uniforme lengte die zich op dezelfde normale afstand bevinden als de werkelijke staven, maar met een zijdelingse offset van nul. De laatste truc is om de afstandsafhankelijkheid van de staaf-deeltje-energie te benaderen met behulp van power-law-functies die oplossingen in gesloten vorm hebben wanneer afstanden lineair variëren met de laterale positie van de eigenlijke staven, zoals het geval is met de vlakke op elkaar inwerkende oppervlakken van gefacetteerde deeltjes.
Nadat al deze vereenvoudigingen zijn aangebracht, kunnen analytische oplossingen voor de energieën tussen de deeltjes worden verkregen, waardoor een computer er doorheen kan waaien. En hoewel het klinkt alsof ze een grote hoeveelheid fouten zouden introduceren, ontdekten de onderzoekers dat de resultaten gemiddeld slechts 8% lager waren dan het daadwerkelijke antwoord voor alle deeltjesconfiguraties, en slechts 25% verschilden in het ergste geval.
Terwijl de onderzoekers voornamelijk met kubussen werkten, lieten ze ook zien dat de aanpak werkt met driehoekige prisma’s, vierkante staven en vierkante piramides. Afhankelijk van de vorm en het materiaal van de nanodeeltjes, kan de modelleringsbenadering invloed hebben op een breed scala aan velden. Zo kunnen zilveren of gouden nanocubes met dicht bij elkaar liggende randen licht bundelen en focussen in minuscule “hotspots”, waardoor betere sensoren kunnen worden gecreëerd of chemische reacties kunnen worden gekatalyseerd.
“Dit is de eerste keer dat iemand een analytisch model heeft voorgesteld voor van der Waals-interacties tussen gefacetteerde deeltjes”, aldus Arya. “Hoewel we het nog moeten toepassen voor het berekenen van krachten of energieën tussen deeltjes binnen moleculaire dynamica of Monte Carlo-simulaties van deeltjesassemblage, verwachten we dat het model dergelijke simulaties met wel tien ordes van grootte zal versnellen.”
Brian Hyun-jong Lee et al. Analytisch van der Waals-interactiepotentieel voor gefacetteerde nanodeeltjes, Nanoschaal Horizons (2020). DOI: 10.1039 / d0nh00526f
Geleverd door Duke University School of Nursing