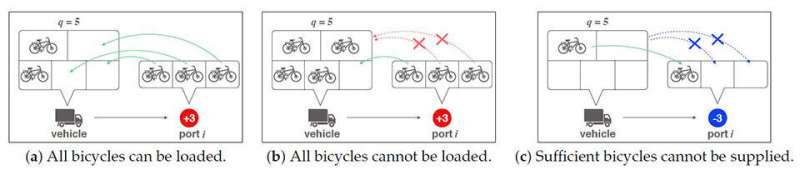
Figuur 1: Voorbeelden van overtredingen van aanbod- en laadbeperkingen. In (a) kan het voertuig voldoen aan de gegeven laadbeperking omdat het de drie overtollige fietsen in haven i kan meenemen. In (b) schendt het voertuig echter de laadbeperking omdat het slechts ruimte heeft voor een van de drie overtollige fietsen in de haven. Evenzo schendt het voertuig in (c) de leveringsbeperking omdat het slechts één fiets kan leveren in poort i, die er drie nodig heeft. In de voorgestelde strategie worden deze beperkingen behandeld als zachte beperkingen bij het formuleren van een probleem. Deze benadering maakt het mogelijk om met een algoritme te zoeken naar zowel haalbare als onhaalbare oplossingsruimten en het zoeken naar bijna-optimale of optimale oplossingen te versnellen. Krediet: Tohru Ikeguchi van de Tokyo University of Science
Fietsdeelsystemen zijn een aantrekkelijke optie geworden om het verkeer in drukke steden te verlichten. Het opnieuw in evenwicht brengen van het aantal fietsen in elke haven naarmate de tijd verstrijkt, is echter essentieel, en het vinden van de optimale routepaden voor de voertuigen die verantwoordelijk zijn voor het opnieuw in evenwicht brengen vormt een combinatorisch optimalisatieprobleem. Nu stellen wetenschappers een innovatief algoritme voor dat zelfs voor een groot aantal havens sneller bijna-optimale oplossingen kan vinden, waardoor de weg wordt vrijgemaakt voor efficiëntere systemen voor het delen van fietsen.
De verkeerscongestie is sinds de jaren vijftig in de grote steden verslechterd dankzij het exorbitante aantal auto’s dat elk jaar wordt verkocht. Helaas omvat het figuurlijke prijskaartje dat aan overmatig verkeer is verbonden een hogere uitstoot van kooldioxide, meer collectief verspilde tijd en verergerde gezondheidsproblemen. Veel gemeenten hebben het verkeersprobleem aangepakt door systemen voor het delen van fietsen te implementeren, waarbij mensen fietsen kunnen lenen van strategisch geplaatste havens en kunnen rijden waar ze willen, zolang ze de fietsen uiteindelijk terugbrengen naar een haven, hoewel niet noodzakelijk de haven van waaruit de fiets werd oorspronkelijk verkregen.
Zoals je misschien wel of niet meteen opmerkt, creëert deze laatste toestemming op zichzelf een nieuw probleem. Wanneer iemand een fiets leent en er geen heen- en terugreis mee maakt, duikt er een extra fiets op in de haven van bestemming, net zoals er een fiets verloren gaat in de haven van herkomst. Naarmate de tijd verstrijkt, wordt de verdeling van fietsen over havens onevenwichtig, wat zowel een overmatige accumulatie van fietsen in bepaalde havens als een gebrek aan fietsen in andere veroorzaakt. Dit probleem wordt over het algemeen aangepakt door periodiek een vloot voertuigen uit te zenden die meerdere fietsen kunnen vervoeren om de havens te herstellen naar hun ‘ideale’ aantal fietsen.
Er is veel onderzoek gedaan naar het probleem van het opnieuw in evenwicht brengen van fietsen met behulp van een wagenpark. Het vinden van de optimale routepaden voor de voertuigen is op zich een zeer complex wiskundig probleem op het gebied van combinatorische optimalisatie. Men moet ervoor zorgen dat de gebruikte optimalisatie-algoritmen in een redelijke tijd tot een voldoende goede oplossing kunnen komen voor een realistisch groot aantal havens en voertuigen. Veel methoden slagen er echter niet in om haalbare oplossingen te vinden wanneer er tegelijkertijd rekening wordt gehouden met meerdere beperkingen, zoals tijd, capaciteit en laad- en losbeperkingen voor de voertuigen (Figuur 1).
Maar wat als we de optimalisatiestrategie de strategieën een beetje zouden laten veranderen om het beste uit moeilijke situaties te halen? In een recente studie gepubliceerd in MDPI’s Toegepaste wetenschappen, een team van wetenschappers suggereerde een innovatieve draai aan het routeringsprobleem van fietsdeelsystemen met behulp van dit concept. Onder leiding van professor Tohru Ikeguchi van de Tokyo University of Science, heeft het team bestaande uit Ph.D. student Honami Tsushima van de Tokyo University of Science en universitair hoofddocent Takafumi Matsuura van het Nippon Institute of Technology, Japan, stelden een nieuwe formulering van het routeringsprobleem voor waarbij de beperkingen die aan de routering worden opgelegd kunnen worden geschonden. Dit maakte het mogelijk om het optimalisatie-algoritme te gebruiken voor het verkennen van wat bekend staat als de ruimte van ‘onhaalbare oplossingen’. Prof. Ikeguchi legt hun redenering uit: “In het echte leven, als een werk binnen een paar minuten door overuren kan worden voltooid, zouden we buiten de tijdslimiet werken. Evenzo, als we slechts vier fietsen vervoeren en er vijf moeten leveren, zouden we leveren nog steeds de vier die we hebben.”
In navolging van deze gedachtegang formuleerden de onderzoekers de “soft constraints”-variant van het routeringsprobleem bij het herbalanceren van fietsen. Door deze benadering te gebruiken, kunnen in plaats van oplossingen die beperkingen schenden volledig worden uitgesloten, deze worden beschouwd als geldige paden die dynamisch aangepaste boetes oplopen en waarmee rekening wordt gehouden bij het beoordelen van mogelijke routeringen. Deze aanpak stelde het team in staat een algoritme te bedenken dat gebruik kan maken van de ruimte van onhaalbare oplossingen om het zoeken naar optimale of bijna-optimale oplossingen te versnellen.
De onderzoekers evalueerden de prestaties van hun methode door middel van numerieke experimenten met benchmarkproblemen, waaronder maximaal 50 poorten en drie voertuigen. De resultaten laten zien dat hun strategie in alle gevallen optimale of bijna optimale oplossingen kon vinden, en dat het algoritme zowel de haalbare als onhaalbare oplossingsruimten efficiënt kon doorzoeken. Dit schetst een betere toekomst voor mensen in steden met verkeersopstoppingen, waarin deelfietsen een aantrekkelijke oplossing kunnen worden. Zoals prof. Ikeguchi opmerkt: “Het is waarschijnlijk dat systemen voor het delen van fietsen zich in de toekomst over de hele wereld zullen verspreiden, en we zijn van mening dat het routeringsprobleem bij het opnieuw in evenwicht brengen van fietsen een belangrijk probleem is dat moet worden opgelost in moderne samenlevingen.”
Honami Tsushima et al, Strategie voor het verkennen van haalbare en onhaalbare oplossingsruimten om een routeprobleem voor het delen van fietsen met meerdere voertuigen op te lossen, Toegepaste wetenschappen (2021). DOI: 10.3390/app11167749
Geleverd door Tokyo University of Science