Hexagonale benaderingen van het metaalgemiddelde helpen de kloof tussen quasikristallen en gemoduleerde structuren te overbruggen

Lange tijd associeerden wetenschappers kristalstructuren met een geordende rangschikking van atomen in een herhalend roosterachtig patroon, omdat ze dachten dat dit de meest stabiele configuratie was. In de jaren 60 onthulden ontwikkelingen in de kristallografie echter materialen die niet in het traditionele model pasten. Deze structuren vertonen een niet-periodiek of niet-herhalend patroon en worden aperiodieke kristallen genoemd.

Er zijn twee soorten aperiodieke kristallen: quasikristallen (QC’s), die geordende maar aperiodieke arrangementen vertonen, en incommensurately (IC) gemoduleerde structuren, waarbij een driedimensionale periodieke roosterstructuur wordt vervormd door ruimtelijke variatie of modulaties. Deze materialen bezitten eigenschappen die verschillen van die van gewone periodieke kristallen, maar de relatie tussen hen blijft grotendeels onontgonnen.

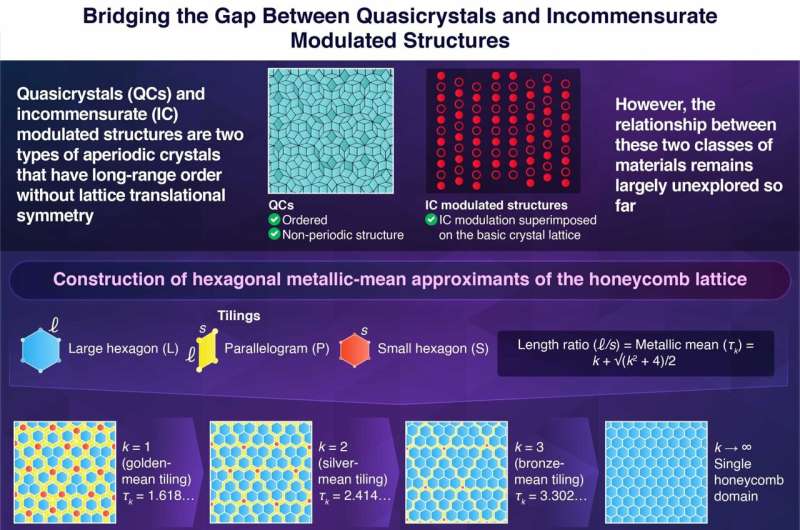
In een onderzoek gepubliceerd in het tijdschrift Natuurcommunicatieonderzoekers onder leiding van universitair hoofddocent Akihisa Koga van de afdeling natuurkunde aan het Tokyo Institute of Technology construeerden een lokaal periodieke honingraatstructuur. Ze rangschikten kleine (S) en grote (L) hexagonale en parallellogram (P) tegels in een tweedimensionale ruimte volgens metallische middelen (generalisaties van de bekende gulden en zilveren verhoudingen), waarbij ze modulaties introduceerden om een ​​honingraattegelpatroon te genereren dat een incommensurabel gemoduleerde structuur vertegenwoordigt.

“We presenteren hexagonale, metallische gemiddelde benaderingen van het honingraatrooster, die de kloof tussen quasikristallen en niet-evenredig gemoduleerde structuren overbruggen”, aldus Koga.

Aperiodiciteit is nauw verbonden met de afstand tussen de atomaire posities in het kristalrooster. In quasikristallen worden deze afstanden gedefinieerd als irrationale getallen die vastzitten aan twee lengteschalen, terwijl ze in IC-gemoduleerde structuren niet vastliggen.

De onderzoekers pasten een aperiodieke benadering toe om de tegels binnen het kristalrooster te rangschikken. Ze varieerden de karakteristieke irrationaliteit in het rooster volgens metallische middelen, zoals de gulden snede, het zilvergemiddelde en het bronsgemiddelde. Ze rangschikten de tegels specifiek zo dat de verhouding tussen de lange lengte (die de grootte van de grote zeshoek vertegenwoordigt) en de korte lengte (gebaseerd op de zijde van de kleine zeshoek en de parallellogramtegel) overeenkwam met verschillende metallische middelen.

Aanvankelijk resulteerde het rangschikken van de tegels door de gulden snede als lengteverhouding te nemen in grote hexagonale tegels begrensd door parallellogrammen en kleinere hexagonale tegels, waardoor een geordende maar niet-periodieke quasikristallijne structuur ontstond. Echter, naarmate de metaal-gemiddelde verhouding toenam, begonnen de grotere hexagonale tegels samen te komen, waardoor honingraatdomeinen ontstonden, beschouwd als een IC-gemoduleerde structuur.

De onderzoekers identificeerden het metallische gemiddelde tegelpatroon in polymeren met behulp van een ISP (I: polyisopreen, S: polystyreen en P: poly(2-vinylpyridine)) triblok terpolymeer. Vanuit de transmissie-elektronenmicroscoopbeelden van het polymeer observeerden ze dat de polymeeropstellingen konden worden weergegeven door L-, P- en S-tegels met een regelmatig gebied van L-tegels in het midden en P-tegels aan de linkerkant. De P-tegels werden geïnterpreteerd als dubbele grenzen die de overgangen tussen verschillende oriëntaties van de L-tegels markeerden.

Dit tegelpatroon werd ook waargenomen in colloïdale deeltjes. De onderzoekers simuleerden het gedrag van 10.000 colloïdale deeltjes die interacteren met een Lennard-Jones-Gauss-potentiaal, en ontdekten dat de ideale opstelling voor de deeltjes een metallische gemiddelde tegel is, bestaande uit op- en neergaande driehoeken.

“Onze studie benadrukt de effectiviteit van aperiodieke approximanten bij het induceren van modulaties binnen zelf-geassembleerde zachte-materiesystemen die de P31m-vlakgroep gebruiken. Meer specifiek gebruikten we de rijen P-tegels als domeingrenzen in het honingraatrooster, waardoor we metallische-gemiddelde hexagonale QC’s en IC-gemoduleerde honingraatroosters overbrugden,” aldus Koga.

“Deze bevindingen bieden inzicht in het domein van zowel aperiodieke kristallen als de bredere implicaties ervan voor domeinwandstructuren in verschillende vakgebieden.”