
Excel heeft ingebouwde functies die u kunt gebruiken om uw kalibratiegegevens weer te geven en een line-of-best-fit te berekenen. Dit kan handig zijn als u een chemisch laboratoriumrapport schrijft of een correctiefactor in een apparaat programmeert.
In dit artikel zullen we bekijken hoe u Excel kunt gebruiken om een grafiek te maken, een lineaire kalibratiecurve uit te zetten, de formule van de kalibratiecurve weer te geven en vervolgens eenvoudige formules met de functies HELLING en INTERCEPT kunt instellen om de kalibratievergelijking in Excel te gebruiken.
Wat is een kalibratiecurve en hoe is Excel nuttig om er een te maken?
Om een kalibratie uit te voeren, vergelijk je de metingen van een apparaat (zoals de temperatuur die een thermometer weergeeft) met bekende waarden die standaarden worden genoemd (zoals het vries- en kookpunt van water). Hiermee kunt u een reeks gegevensparen maken die u vervolgens gebruikt om een kalibratiecurve te ontwikkelen.
Een tweepuntskalibratie van een thermometer met behulp van het vriespunt en het kookpunt van water zou twee dataparen hebben: een vanaf het moment dat de thermometer in ijswater wordt geplaatst (32°F of 0°C) en één in kokend water (212°F of 100°C). Wanneer u die twee gegevensparen als punten plot en een lijn daartussen trekt (de kalibratiecurve), en aangenomen dat de respons van de thermometer lineair is, kunt u elk punt op de lijn kiezen dat overeenkomt met de waarde die de thermometer weergeeft, en u kan de overeenkomstige “echte” temperatuur vinden.
De lijn vult dus in wezen de informatie tussen de twee bekende punten voor u in, zodat u redelijk zeker kunt zijn bij het schatten van de werkelijke temperatuur wanneer de thermometer 57,2 graden aangeeft, maar wanneer u nog nooit een ‘standaard’ hebt gemeten die overeenkomt met dat lezen.
Excel heeft functies waarmee u de gegevensparen grafisch in een grafiek kunt plotten, een trendlijn (kalibratiecurve) kunt toevoegen en de vergelijking van de kalibratiecurve op de kaart kunt weergeven. Dit is handig voor een visuele weergave, maar u kunt ook de formule van de lijn berekenen met de functies HELLING en INTERCEPT van Excel. Wanneer u deze waarden in eenvoudige formules invoert, kunt u automatisch de “ware” waarde berekenen op basis van elke meting.
Laten we naar een voorbeeld kijken
Voor dit voorbeeld zullen we een kalibratiecurve ontwikkelen uit een reeks van tien dataparen, elk bestaande uit een X-waarde en een Y-waarde. De X-waarden zullen onze “standaarden” zijn en ze kunnen van alles vertegenwoordigen, van de concentratie van een chemische oplossing die we meten met een wetenschappelijk instrument tot de invoervariabele van een programma dat een marmer-lanceermachine bestuurt.
De Y-waarden zijn de “reacties” en vertegenwoordigen de aflezing van het instrument bij het meten van elke chemische oplossing of de gemeten afstand van hoe ver van de lanceerinrichting de knikker landde met behulp van elke invoerwaarde.
Nadat we de kalibratiecurve grafisch hebben weergegeven, zullen we de functies HELLING en INTERCEPT gebruiken om de formule van de kalibratielijn te berekenen en de concentratie van een ‘onbekende’ chemische oplossing te bepalen op basis van de uitlezing van het instrument of beslissen welke invoer we het programma moeten geven zodat de marmer landt op een bepaalde afstand van de draagraket.
Stap één: maak uw diagram
Ons eenvoudige voorbeeldspreadsheet bestaat uit twee kolommen: X-waarde en Y-waarde.

Laten we beginnen met het selecteren van de gegevens die in de grafiek moeten worden uitgezet.
Selecteer eerst de kolomcellen ‘X-waarde’.

Druk nu op de Ctrl-toets en klik vervolgens op de kolomcellen van de Y-waarde.

Ga naar het tabblad “Invoegen”.

Navigeer naar het menu “Grafieken” en selecteer de eerste optie in de vervolgkeuzelijst “Scatter”.

Selecteer de serie door op een van de blauwe punten te klikken. Eenmaal geselecteerd, schetst Excel dat de punten worden geschetst.

Klik met de rechtermuisknop op een van de punten en selecteer vervolgens de optie “Trendlijn toevoegen”.

Er verschijnt een rechte lijn op de kaart.

Aan de rechterkant van het scherm verschijnt het menu “Trendlijn opmaken”. Vink de vakjes aan naast ‘Vergelijking weergeven op diagram’ en ‘R-kwadraatwaarde weergeven op diagram’. De R-kwadraatwaarde is een statistiek die aangeeft hoe nauw de lijn bij de gegevens past. De beste R-kwadraatwaarde is 1.000, wat betekent dat elk datapunt de lijn raakt. Naarmate de verschillen tussen de datapunten en de lijn groter worden, daalt de r-kwadraatwaarde, waarbij 0.000 de laagst mogelijke waarde is.

De vergelijking en de R-kwadraat-statistiek van de trendlijn verschijnen op de grafiek. Merk op dat de correlatie van de gegevens erg goed is in ons voorbeeld, met een R-kwadraatwaarde van 0,988.
De vergelijking heeft de vorm “Y = Mx + B”, waarbij M de helling is en B het snijpunt van de y-as van de rechte lijn.

Nu de kalibratie is voltooid, gaan we werken aan het aanpassen van de grafiek door de titel te bewerken en astitels toe te voegen.
Om de titel van het diagram te wijzigen, klikt u erop om de tekst te selecteren.

Typ nu een nieuwe titel die de grafiek beschrijft.

Om titels aan de x-as en y-as toe te voegen, navigeert u eerst naar Hulpmiddelen voor grafieken> Ontwerp.

Navigeer nu naar Axis Titles> Primary Horizontal.
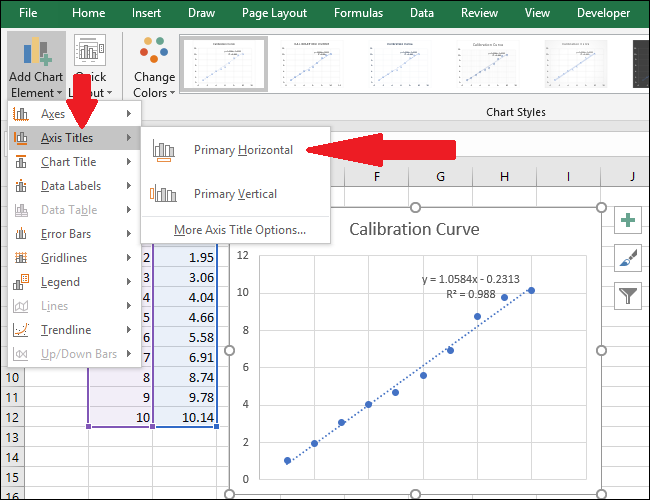
Om de naam van de astitel te wijzigen, selecteert u eerst de tekst en voert u vervolgens een nieuwe titel in.

Ga nu naar Axis Titles> Primary Vertical.

Er verschijnt een astitel.

Hernoem deze titel door de tekst te selecteren en een nieuwe titel in te typen.

Je diagram is nu compleet.

Stap twee: Bereken de lijnvergelijking en de R-kwadraatstatistiek
Laten we nu de lijnvergelijking en de R-kwadraatstatistiek berekenen met behulp van de ingebouwde functies HELLING, INTERCEPT en CORREL van Excel.
Aan ons blad (in rij 14) hebben we titels toegevoegd voor die drie functies. We voeren de daadwerkelijke berekeningen uit in de cellen onder die titels.
Eerst zullen we de HELLING berekenen. Selecteer cel A15.

Navigeer naar Formules> Meer functies> Statistisch> HELLING.

Selecteer of typ de cellen in de kolom X-waarde in het veld “Known_xs”. De volgorde van de velden ‘Known_ys’ en ‘Known_xs’ is van belang in de functie SLOPE.

Klik OK.” De uiteindelijke formule in de formulebalk zou er als volgt uit moeten zien:
=SLOPE(C3:C12,B3:B12)
Merk op dat de waarde die wordt geretourneerd door de functie SLOPE in cel A15 overeenkomt met de waarde die wordt weergegeven in het diagram.

Selecteer vervolgens cel B15 en navigeer vervolgens naar Formules> Meer functies> Statistisch> INTERCEPT.

Selecteer of typ de cellen in de kolom X-waarde voor het veld “Known_xs”. De volgorde van de velden ‘Known_ys’ en ‘Known_xs’ is ook van belang in de INTERCEPT-functie.

Klik OK.” De uiteindelijke formule in de formulebalk zou er als volgt uit moeten zien:
=INTERCEPT(C3:C12,B3:B12)
Merk op dat de waarde die door de INTERCEPT-functie wordt geretourneerd, overeenkomt met het y-snijpunt dat in het diagram wordt weergegeven.

Selecteer vervolgens cel C15 en navigeer naar Formules> Meer functies> Statistisch> CORREL.

Selecteer of typ de andere van de twee celbereiken voor het veld “Array2”.

Klik OK.” De formule zou er als volgt uit moeten zien in de formulebalk:
=CORREL(B3:B12,C3:C12)
Merk op dat de waarde die wordt geretourneerd door de CORREL-functie niet overeenkomt met de “r-kwadraat” -waarde in het diagram. De CORREL-functie retourneert “R”, dus we moeten het kwadrateren om “R-squared” te berekenen.

Klik in de functiebalk en voeg “^ 2” toe aan het einde van de formule om de waarde die door de CORREL-functie wordt geretourneerd, te kwadrateren. De voltooide formule zou er nu als volgt uit moeten zien:
=CORREL(B3:B12,C3:C12)^2
Druk op Enter.

Na het wijzigen van de formule, komt de “R-kwadraat” -waarde nu overeen met die in de grafiek.

Stap drie: stel formules in om snel waarden te berekenen
Nu kunnen we deze waarden gebruiken in eenvoudige formules om de concentratie van die “onbekende” oplossing te bepalen of welke invoer we in de code moeten invoeren zodat de knikker een bepaalde afstand vliegt.
Met deze stappen worden de formules opgesteld die nodig zijn om een X-waarde of een Y-waarde in te voeren en de bijbehorende waarde te krijgen op basis van de kalibratiecurve.

De vergelijking van de best passende lijn heeft de vorm ‘Y-waarde = SLOPE * X-waarde + INTERCEPT’, dus het oplossen van de ‘Y-waarde’ wordt gedaan door de X-waarde en HELLING te vermenigvuldigen en vervolgens het toevoegen van de INTERCEPT.

Als voorbeeld plaatsen we nul als de X-waarde. De teruggegeven Y-waarde moet gelijk zijn aan het INTERCEPT van de best passende lijn. Het komt overeen, dus we weten dat de formule correct werkt.

Het oplossen van de X-waarde op basis van een Y-waarde doe je door het INTERCEPT af te trekken van de Y-waarde en het resultaat te delen door de HELLING:
X-value=(Y-value-INTERCEPT)/SLOPE

Als voorbeeld hebben we de INTERCEPT als Y-waarde gebruikt. De geretourneerde X-waarde moet gelijk zijn aan nul, maar de geretourneerde waarde is 3.14934E-06. De geretourneerde waarde is niet nul omdat we per ongeluk het INTERCEPT-resultaat hebben afgekapt bij het typen van de waarde. De formule werkt echter correct, omdat het resultaat van de formule 0,00000314934 is, wat in wezen nul is.

U kunt elke gewenste X-waarde invoeren in de eerste cel met dikke randen en Excel berekent automatisch de bijbehorende Y-waarde.

Als u een Y-waarde invoert in de tweede cel met dikke randen, krijgt u de bijbehorende X-waarde. Deze formule is wat je zou gebruiken om de concentratie van die oplossing te berekenen of welke input nodig is om de knikker een bepaalde afstand te lanceren.

In dit geval leest het instrument “5”, zodat de kalibratie een concentratie van 4,94 suggereert of we willen dat de knikker vijf afstandseenheden aflegt, dus de kalibratie suggereert dat we 4,94 invoeren als de invoervariabele voor het programma dat de knikkerwerper bestuurt. We kunnen redelijk zeker zijn van deze resultaten vanwege de hoge R-kwadraatwaarde in dit voorbeeld.